RUMUS BANGUN DATAR

1. PERSEGI

 

Persegi adalah bangun datar yang mempunyai 4 sisi yang sama panjang, yang disimbolkan dengan huruf "s". Untuk mencari luas (L) dan kelilingnya (K) dapat ditentukan dengan rumus:

L = s x s ;

K = 4 x s

contoh: jika diketahui sisi dari bangun persegi adalah 3 cm, maka tentukan luas dan kelilingnya!

jawab: untuk mencari luasnya yaitu, L = s x s = 3 x 3 = 9, sedangkan untuk kelilingnya K = 4 x 3 = 12. Jadi, luasnya yaitu 9 cm dan memiliki keliling 12 cm

 2. PERSEGI PANJANG

Persegi panjang adalah bangun datar segiempat yang keempat sudutnya siku-siku dan sisi-sisi yang berhadapan sama panjang.

Persegi panjang memiliki sifat-sifat sebagai berikut. 

1) Mempunyai empat sisi, dengan sisi-sisi yang berhadapan sama

panjang dan sejajar 

2) Keempat sudutnya sama besar dan merupakan sudut siku-siku

3) Diagonal-diagonalnya sama panjang dan saling membagi dua sama

panjang

4) Dapat menempati bingkainya dengan dua cara

5) Mempunyai dua sumbu simetri

Rumus :
Keliling (K) : 2 x (Panjang + Lebar)
Luas (L) : Panjang x Lebar

3. SEGITIGA

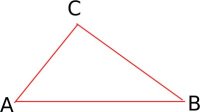
Segitiga adalah sebuah bangun datar yang dibatasi oleh tiga buah sisi dan mempunyai tiga buah titik sudut.

Sisi segitiga ABC diatas adalah AB, BC dan AC. Sedangkan ∠ BAC, ∠ ABC, dan ∠ ACB disebut sudut segitiga ABC. Besar jumlah ketiga sudut tersebut adalah adalah .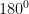

Keliling Segitiga adalah jumlah panjang ketiga sisinya atau

K = a + b + c

Rumus Luas Segitiga :

L = 1/2 x alas x tinggi

Jenis-jenis Segitiga

Jenis-jenis suatu segitiga dapat ditinjau berdasarkan :

a. Panjang sisi-sisinya

           1. Segitiga sebarang adalah segitiga yang sisi-sisinya tidak sama panjang. Pada gambar dibawah ini  merupakan

                segitiga sembarang dimana AB tidak sama dengan BC Tidak sama dengan AC

          2. Segitiga sama kaki
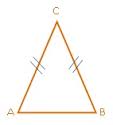
          Segitiga sama kaki adalah segitiga yang mempunyai dua buah sisi sama panjang. Pada gambar dibawah ini                      merupakan segitiga sama kaki ABC dengan AB = BC.

          3. Segitiga sama sisi

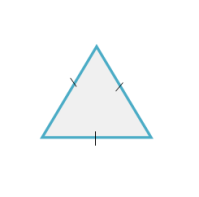
                Segitiga sama sisi adalah segitiga yang memiliki tiga buah sisi sama panjang dan tiga buah sudut sama besar. Segitiga  pada Gambar dibawah ini merupakan segitiga sama sisi.

b. Besar sudut-sudutnya

1. Segitiga lancip

           Segitiga lancip adalah segitiga yang ketiga sudutnya merupakan sudut lancip, sehingga sudut-sudut yang terdapat pada segitiga tersebut besarnya antara 0 derajat  dan 90 derajat . Pada Gambar dibawah ini, ketiga sudut pada Δ ABC adalah sudut  lancip.

     2. Segitiga tumpul

         Segitiga tumpul adalah segitiga yang salah satu sudutnya merupakan sudut tumpul. Pada  Δ ABC di samping, sudut  ABC adalah  sudut tumpul.

     3. Segitiga siku-siku

          Segitiga siku-siku adalah segitiga yang salah satu sudutnya merupakan sudut siku-siku (besarnya 90 derajat). Pada Gambar di bawah ini, Δ ABC siku-siku di titik C.

c. Panjang sisi dan besar sudutnya.

1.  Segitiga siku-siku sama kaki         

           Segitiga siku-siku sama kaki adalah segitiga yang kedua sisinya sama panjang dan salah satu sudutnya merupakan sudut siku- siku (90 derajat).

           Pada Gambar di bawah ini, Δ abc siku-siku di titik b, dengan ab = ac.

       

     2. Segitiga tumpul sama kaki

          Segitiga tumpul sama kaki adalah segitiga yang kedua sisinya sama panjang dan salah satu sudutnya merupakan sudut tumpul.

          Sudut tumpul Δ PQR pada Gambar di bawah ini adalah sudut  P, dengan PR = PQ.

Baca Juga : Rumus Bangun Datar II