Bisakah kalian memasukkan Kota Surabaya ke dalam beberapa kategori/kelompok yang berbeda-beda? Pertama, kalian mungkin mengkategorikan Kota Surabaya sebagai salah satu ibu kota provinsi di Indonesia. Kedua, kalian juga dapat mengkategorikan Kota Surabaya sebagai salah satu kota besar di Indonesia. Dengan cara lain, kalian juga dapat mengkategorikan Kota Surabaya sebagai salah satu kota terpadat di Indonesia. Pada pembahasan ini kita akan membahas bagaimana cara mengelompokkan atau mengklasifikasikan beberapa objek.
Kita sering menjumpai himpunan dalam berbagai cara di sekitar kita dan dalam kehidupan sehari-hari. Himpunan adalah kumpulan dari objek-objek, yang disebut elemen atau anggota himpunan, dan terdefinisi dengan jelas. Maksud dari terdefinisi dengan jelas adalah bahwa anggota-anggota himpunan dapat ditentukan secara jelas. Sebagai contoh, kumpulan dari semua provinsi-provinsi di Indonesia per Oktober 2014 merupakan suatu himpunan karena kita dapat menentukan dengan jelas anggota-anggota dari himpunan tersebut. Seperti kita tahu, Jawa Timur dan 34 provinsi
lainnya merupakan anggota dari himpunan tersebut.
lainnya merupakan anggota dari himpunan tersebut.
Akan tetapi, apakah kumpulan dari 5 album musik terbaik merupakan suatu himpunan? Karena kata terbaik dapat diinterpretasikan secara berbeda oleh orang yang berbeda, maka kumpulan tersebut tidak terdefinisi dengan jelas. Akibatnya, kumpulan dari 5 album musik terbaik bukan suatu himpunan.
Untuk menyatakan suatu himpunan dapat digunakan 3 cara:
(1) dengan kata-kata atau deskripsi,
(2) dengan mendaftar, dan
(3) dengan notasi pembentuk himpunan.
Cara menyatakan himpunan dengan kata-kata dapat diilustrasikan oleh contoh 1 berikut.
Contoh 1: Deskripsi dari Suatu Himpunan
Nyatakan dengan kata-kata suatu himpunan yang anggota-anggotanya Senin, Selasa, Rabu, Kamis, Jumat, Sabtu, dan Minggu.
Jawaban Himpunan dari nama-nama hari dalam satu minggu.
Mendaftar anggota-anggota suatu himpunan ke dalam sepasang kurung kurawal, { }, merupakan cara menyatakan himpunan dengan mendaftar. Sepasang kurung kurawal tersebut merupakan notasi yang perlu karena kurung kurawal tersebut mengidentifikasikan konten yang dimaksud sebagai himpunan. Sebagai contoh, {1, 2, 3} merupakan notasi untuk himpunan yang memiliki anggota-anggota 1, 2, dan 3. Akan tetapi (1, 2, 3) dan [1, 2, 3] bukan suatu himpunan karena simbol ( ) dan [ ] tidak mengindikasikan suatu himpunan. Dalam penulisan himpunan dengan mendaftar, tanda koma digunakan untuk memisahkan anggota-anggota dari himpunan tersebut. Urutan dari anggota-anggota himpunan yang terdaftar tidak penting. Sehingga himpunan {1, 2, 3} dapat juga dituliskan sebagai {3, 2, 1} atau {2, 3, 1}.
Secara umum, himpunan dinamai dengan menggunakan huruf kapital. Sebagai contoh, himpunan bilangan asli biasanya dinamai dengan N.
Definisi: Bilangan Asli
N = {1, 2, 3, 4, 5, …}
Tiga titik setelah bilangan 5, yang disebut sebagai elipsis, mengindikasikan bahwa anggota-anggota dalam himpunan tersebut akan berkelanjutan dalam pola yang sama. Apabila tanda elipsis tersebut diikuti oleh anggota/elemen terakhir, maka anggota himpunan tersebut akan berkelanjutan dengan pola yang sama sampai anggota terakhir tersebut. Notasi ini dapat diilustrasikan oleh contoh 2.1 berikut.
Contoh 2: Menyatakan Himpunan dengan Cara Mendaftar
Tulislah himpunan-himpunan berikut dengan cara mendaftar.
Himpunan A adalah himpunan bilangan asli yang kurang dari 6.
Himpunan B adalah himpunan bilangan asli yang kurang dari atau sama dengan 100.
Himpunan P adalah himpunan planet-planet dalam tata surya.
Pembahasan
Bilangan asli yang kurang dari 6 adalah 1, 2, 3, 4, dan 5. Sehingga, himpunan A dapat dinyatakan dengan A = {1, 2, 3, 4, 5}.
B = {1, 2, 3, 4, … , 80}. Bilangan 80 setelah elipsis mengindikasikan bahwa anggota-anggota B berkelanjutan dengan pola yang sama sampai 80.
P = {Merkurus, Venus, Bumi, Mars, Jupiter, Saturnus, Uranus, Neptunus}. Pluto bukan anggota dari P karena pada Agustus 2006 Pluto digolongkan kembali sebagai planet kerdil.
Contoh 3: Kata Inklusif
Tulislah himpunan-himpunan berikut dengan cara mendaftar.
Himpunan bilangan asli di antara 3 dan 8.
Himpunan bilangan asli di antara 3 dan 8, inklusif.
Pembahasan
A = {4, 5, 6, 7}
B = {3, 4, 5, 6, 7, 8}. Perhatikan bahwa kata inklusif mengindikasikan bahwa bilangan-bilangan 3 dan 8 merupakan anggota B.
Selanjutnya kita akan membahas keanggotan dari suatu himpunan dan simbolnya. Perhatikan ilustrasi berikut.
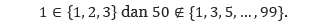
Dari ilustrasi di atas, kita dapat menyatakan bahwa 1 anggota dari {1, 2, 3} dan 50 bukan anggota dari {1, 3, 5, … , 99}.
Notasi pembentuk himpunan digunakan untuk menyimbolkan suatu himpunan. Notasi pembentuk himpunan biasanya digunakan di aljabar. Perhatikan contoh penulisan notasi pembentuk himpunan berikut.

Perhatikan contoh penulisan himpunan ke dalam notasi pembentuk himpunan berikut.
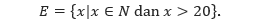
Pernyataan di atas dapat dibaca sebagai “E adalah himpunan semua x sedemikian sehingga x bilangan asli dan x lebih besar dari 20.” Sehingga, himpunan E tersebut apabila dituliskan dengan cara mendaftar akan menjadi, E = {21, 22, 23, … }.
Contoh 4: Penggunaan Notasi Pembentuk Himpunan
Tulislah himpunan-himpunan berikut ke dalam notasi pembentuk himpunan.
B = {3, 4, 5, … , 97}
C = {51, 53, 55, … , 149}
D = {M, A, T, E, I, K}
Pembahasan
Himpunan B memiliki anggota-anggota 3, 4, 5, … , 97, yaitu bilangan-bilangan asli di antara 2 dan 98. Sehingga apabila dituliskan ke dalam bentuk notasi pembentuk himpunan akan menjadi,
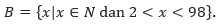
Himpunan C memiliki anggota-anggota 51, 53, 55, … , 149, yaitu bilangan gasal di antara 51 dan 149. Karena bilangan gasal dapat dinyatakan dengan 2x – 1 untuk x bilangan asli maka himpunan C dapat dinyatakan dengan,
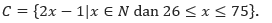
D = {x | x huruf-huruf penyusun kata “MATEMATIKA”}.
Suatu himpunan dikatakan hingga apabila himpunan tersebut tidak memiliki anggota atau himpunan tersebut memiliki anggota yang banyaknya berupa bilangan asli. Himpunan F = {3, 6, 12, 24, 48, 96} merupakan himpunan hingga karena banyaknya anggota himpunan F adalah 6 yang merupakan anggota bilangan asli. Sedangkan himpunan yang tidak hingga disebut himpunan tak hingga. Salah satu contoh himpunan tak hingga adalah himpunan bilangan asli.
Konsep penting lainnya dari himpunan adalah kesamaan dari himpunan.
Definisi: Himpunan-himpunan Sama
Himpunan A sama dengan himpunan B, disimbolkan dengan A = B, jika dan hanya jika himpunan A dan himpunan B memuat anggota-anggota yang tepat sama.
Sebagai contoh, jika A = {1, 2, 3} dan B = {2, 1, 3} maka A = B karena himpunan-himpunan tersebut memuat anggota-anggota yang tepat sama. Urutan anggota-anggota himpunan tersebut tidaklah penting. Jika dua himpunan sama, maka kedua himpunan tersebut memiliki banyak anggota yang sama. Banyaknya anggota dari suatu himpunan disebut sebagai bilangan kardinal.
Definisi: Bilangan Kardinal
Bilangan kardinal dari himpunan A, disimbolkan dengan n(A), adalah banyaknya angota himpunan A.
Himpunan-himpunan A = {3, 9, 27} dan B = {17, Malang, Motor} memiliki bilangan kardinal 3, yaitu n(A) = n(B) = 3. Kita dapat menyatakan bahwa himpunan-himpunan A dan B memiliki bilangan kardinal yang sama.
Himpunan-himpunan yang bilangan kardinalnya sama disebut sebagai himpunan-himpunan yang ekuivalen.
Definisi: Himpunan-himpunan Ekuivalen
Himpunan A ekuivalen dengan himpunan B jika dan hanya jika n(A) = n(B).
Semua himpunan-himpunan yang sama merupakan himpunan-himpunan yang ekuivalen. Akan tetapi himpunan-himpunan yang ekuivalen belum tentu merupakan himpunan-himpunan yang sama. Himpunan K = {x, y, z} dan L = {merah, buku, piring} merupakan dua himpunan yang ekuivalen, karena bilangan kardinal dari kedua himpunan tersebut adalah 3. Karena anggota-anggota himpunan K dan L berbeda, maka kedua himpunan tersebut bukanlah himpunan-himpunan yang sama.
Himpunan Kosong (Null Or Empty Set)
Beberapa himpunan tidak memiliki anggota, salah satu contohnya adalah himpunan dinosaurus yang hidup di tahun 2013.
Definisi: Himpunan Kosong
Suatu himpunan yang tidak memiliki anggota disebut himpunan kosong dan disimbolkan sebagai { } atau Ø.
Perhatikan bahwa {Ø} bukan merupakan himpunan kosong. Himpunan ini memiliki anggota Ø dan bilangan kardinalnya adalah 1. Himpunan {0} juga bukan himpunan kosong karena himpunan tersebut beranggotakan 0. Himpunan {0} juga memiliki bilangan kardinal 1.
Contoh 5: Penyelesaian Bilangan Asli
Tentukan himpunan bilangan asli yang memenuhi persamaan x + 5 = 0.
Pembahasan Bilangan yang memenuhi pernyataan tersebut haruslah bilangan asli yang membuat persamaan tersebut bernilai benar. Hanya bilangan –2 yang memenuhi persamaan tersebut. Karena –2 bukan bilangan asli, maka himpunan penyelesaian dari persamaan tersebut adalah { } atau Ø.
Himpunan Semesta
Himpunan yang penting lainnya dalam konsep himpunan adalah himpunan semesta (universal set).
Definisi: Himpunan Semesta
Himpunan semesta, disimbolkan dengan S, adalah suatu himpunan yang memuat semua anggota dari pembicaraan tertentu.
Ketika suatu himpunan semesta diberikan, hanya anggota-anggota himpunan semestalah yang harus diperhatikan untuk menyelesaikan suatu permasalahan. Sebagai contoh, jika himpunan semesta dari permasalahan tertenu adalah S = {1, 2, 3, … , 10}, maka hanya bilangan asli 1 sampai 10 yang harus digunakan dalam permasalahan tersebut.
Post a Comment